Vega de una opción y los Efectos de la Volatilidad Implícita en las Opciones
Vega de una opción es uno de los parámetros al que deberíamos prestarle especial atención a la hora de lidiar con un mercado de opciones que se encuentre muy volátil.
Al igual que con otras griegas como delta o theta, la griega vega es una expresión que se calcula a través del modelo de Black Scholes para opciones financieras.
En esta guía vamos a aprender como usar la vega de una opción, veremos qué es y cómo trabajar con ella.
Table of Contents
Comencemos por lo más básico…
¿Qué es la vega de una opción?
La vega de una opción es una letra griega que nos va a permitir medir cuanto varía la prima de nuestro contrato cuando la volatilidad implícita de la acción subyacente varía.
La vega de una opción nos va a ser muy útil para observar los efectos de la volatilidad en aquellas opciones que sólo tienen valor extrínseco, porque son precisamente estas a las que más afecta la volatilidad.
Es especialmente útil usar la vega de una opción en aquellas compañías que tienen una volatilidad alta y variable, porque con ello nos podremos hacer una idea de cuánto va a variar el precio de nuestra opción financiera.
¿Cómo funciona la vega de una opción?
Veamos un ejemplo para ver cómo funciona la vega de una opción financiera en un operación.
Supongamos que queremos abrir una operación de opciones sobre acciones sobre la empresa Fiserv.
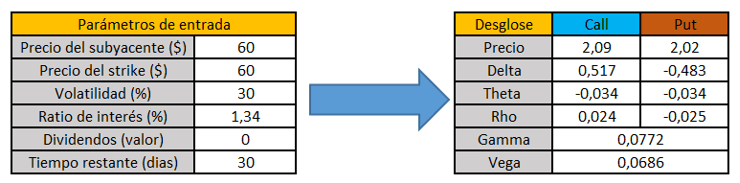
Hoy en día, el precio del activo subyacente, o lo que es lo mismo, el precio de la acción es de 60$. Si le echamos un vistazo a las cadenas de opciones, veremos que comprar un contrato de opciones put cuyo precio de strike es de 60$ es una buena decisión.
La volatilidad implícita de la opción financiera que hemos escogido está en torno al 30%.
En la imagen anterior podemos ver el valor de vega de nuestra opción financiera, el cual nos indica que, si la volatilidad implícita de este contrato se incremente o disminuye en un punto porcentual, el valor de la prima de la opción variará el valor de vega. Así pues, supongamos que la volatilidad se incrementa en un punto.
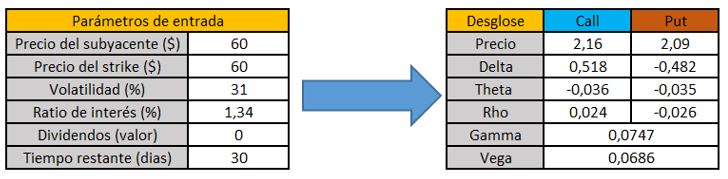
Efectivamente, en ambos casos, si dejamos sin cambiar el resto de los parámetros y sólo manipulamos la volatilidad implícita, podemos ver cómo ha variado la prima de la opción put, pasando de valer 2.02 $ a 2.09 $, siendo el valor de vega de 0.07 aproximadamente.
¿Acabas de iniciarte en opciones o todavía encuentras algunos conceptos confusos?  Con la serie de libros de Trading de Opciones para Todos aprenderás todo lo que necesitas saber para dominar el mercado de opciones |
¿Es el efecto de la vega de una opción financiera aditivo?
Si, el efecto de vega de una opción es aditivo. Tomemos el mismo ejemplo que en el caso anterior.
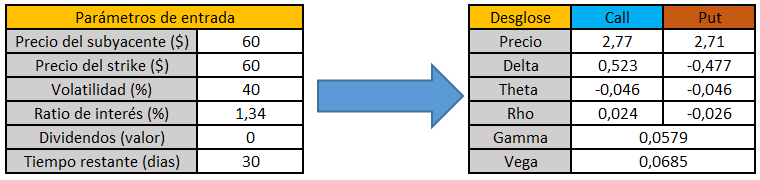
Si, en lugar de un punto, la volatilidad se hubiera incrementado en diez, significaría que la vega de la opción ahora tendría un efecto acumulado de 0.685$. Veamos la calculadora de nuevo para ver si esto es así…
Cuando la volatilidad se encontraba a valor de 30%, la prima de la opción put valía 2.02$ y ahora, con una volatilidad de diez puntos mayor, la prima se ha incrementado a 2.71$.
La diferencia entre las primas es de 0.685$, que es precisamente lo que nos proporcionaba la vega de la opción.
¿Cuándo alcanza vega de una opción financiera su valor más alto?
Normalmente, encontraremos el valor de vega en su punto más alto cuando el precio de la acción subyacente y el precio de ejercicio sean el mismo.
En otras palabras, la vega de una opción alcanza su máximo cuando tratamos con opciones que se encuentran At The Money.
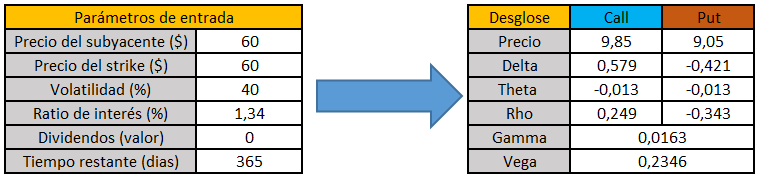
Además, la vega de una opción también será mayor en función del tiempo restante para el vencimiento. A mayor tiempo, mayor vega. Vamos a compararlo siguiendo el mismo ejemplo, pero incrementado el numero de días hasta 365.
Como se puede ver, la vega de la opción ha cambiado de valer 0.0685 a 0.2346 y la única razón es que hemos aumentado el número de días hasta el vencimiento.
¿Puede la vega de una opción ser negativa?
No, vega no puede ser negativa. La razón es sencilla. Si la volatilidad se incrementa en nuestro contrato, la única cosa que puede ocurrir es que la prima de la opción se incremente con ella.
Si la volatilidad cae, en ambos contratos se verá una caída de la prima de la opción.
La diferencia con delta, por ejemplo, es la siguiente. Si el precio del activo subyacente se incrementa, la opción call incrementara su valor debido a que delta es positiva.
Sin embargo, en la opción put la prima va a caer porque delta es negativa. Para que una opción put incremente su valor de delta, el activo subyacente debe perder valor.
Con la vega de una opción financiera, esta situación no ocurre y es precisamente esa la razón por la que no puede ser negativa.
¿Necesitas una Calculadora que te ayude a crear y analizar cualquier estrategia en tiempo record? |
¿Cómo calcular la vega de una opción financiera?
La manera de calcular la vega de una opción es a través de una expresión dada por el modelo de Black Scholes. En primer lugar, es necesario obtener todos los parámetros del modelo matemático.
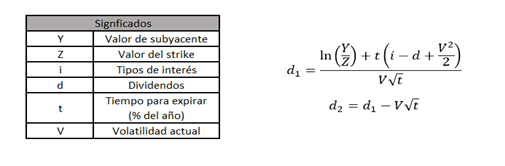
En primer lugar, vamos a necesitar dos parámetros auxiliares llamados d1 y d2. Estos se obtiene como sigue:
En este caso “ln” es el logaritmo Neperiano y “t” es el porcentaje de tiempo hasta el vencimiento, que se calculaba dividiendo el número de días al vencimiento entre el número de días del año.
¿Cuál es la fórmula de la vega de una opción?
La fórmula es la siguiente:
En este caso, y al contrario que ocurre con delta o con theta, la formula de vega de una opción financiera es común para opciones call como para opciones put. Si no quieres calcularlas por ti mismo, puedes descargar nuestra calculadora de opciones gratuita tras acceder a nuestra Guía de Opciones aquí:
Reflexión final sobre la griega Vega en opciones
Con esto, ya hemos visto cómo la griega vega afecta el cambio de la volatilidad implícita en las opciones financieras y cómo tenerlo en cuenta a la hora de introducir los datos en la calculadora, los cuales, recordemos, deberemos tomar de la volatilidad implícita del lado comprador o vendedor, según qué intención tengamos de operar.
Recordemos que la vega de una opción es sólo una de las seis griegas más que existen, y que cada una nos permitirá medir la variación de los precios de la prima de cada uno de los parámetros que lo forman.
Entre otras griegas, nos podemos encontrar con theta o rho, las cuales nos darán información muy útil sobre el factor del tiempo o sobre cómo afecta los tipos de interés en los precios de la prima de la opción, respectivamente.
