¿Qué es el modelo de Black Scholes? – Una Guía Completa para Entender Como Como se Forma el Precio de Una Opción
Una de las primeras preguntas que nos hacemos a la hora de aprender y de entender cómo funciona el trading de opciones es qué es el modelo de Black Scholes y para qué se usa y la respuesta es simple: sirve para calcular los precios de las primas de las opciones.
Aquí vamos a explicar qué es el modelo de Black Scholes exactamente, para qué se usa y cuales son los principales factores que están relacionados en la formación de la prima de una opción.
También veremos aspectos importantes como la deducción de la ecuación de Black Scholes, así como calcular Black Scholes, su fórmula y cómo replicarla en Excel.
Table of Contents
¿Qué es el modelo de Black Scholes en opciones financieras?
El modelo de Black Scholes es un modelo matemático que nos va a proporcionar el precio o la prima de una opción financiera, para cualquier tipo de activo en cualquier tipo de mercado de opciones, tanto para opciones call y puts y para cualquier precio de strike y fecha de vencimiento en una cadena de opciones.
¿Por qué es el modelo Black and Scholes tan importante?
La razón por la que el modelo Black Scholes es tan importante es debido a que es capaz de proporcionar la prima de cualquier contrato de opciones, ya sea una opción de estilo Europeo o Americano.
La buena noticia, es que este mismo modelo se emplea en opciones sobre acciones, sobre índices o sobre futuros.
¿Necesitas una Calculadora que te ayude a crear y analizar cualquier estrategia en tiempo record? |
¿Cómo funciona el modelo Black Scholes?
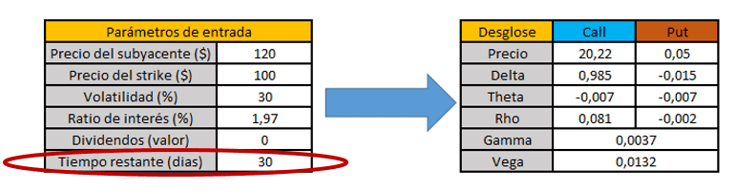
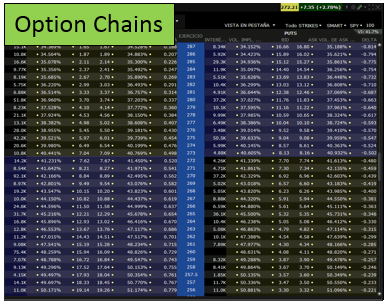
El modelo Black and Scholes funciona a través de la combinación de seis parámetros que se pueden obtener en las cadenas de opciones.
Para poder calcular el valor exacto de la prima de la opción sobre un activo en particular, vamos a necesitar dichos parámetros.
Si necesitas obtener una calculadora que tenga incluido el modelo de Black and Scholes directamente en formato Excel, puedes descargarte la nuestra, junto con la Guía de Opciones gratuita aquí:
Los seis parámetros necesarios en la ecuación de Black Scholes en opciones financieras
1. El precio del subyacente
El primer parámetro más básico es el precio del subyacente con el que estamos trabajando en el momento actual.
Si, por ejemplo, estamos tratando con las opciones sobre la acción de Microsoft, el precio del subyacente que debemos introducir en el modelo de Black Scholes no es otro que el precio actual de Microsoft, en el momento en el que vayamos a realizar el cálculo.
precio de ejercicio» width=»587″ height=»598″ />
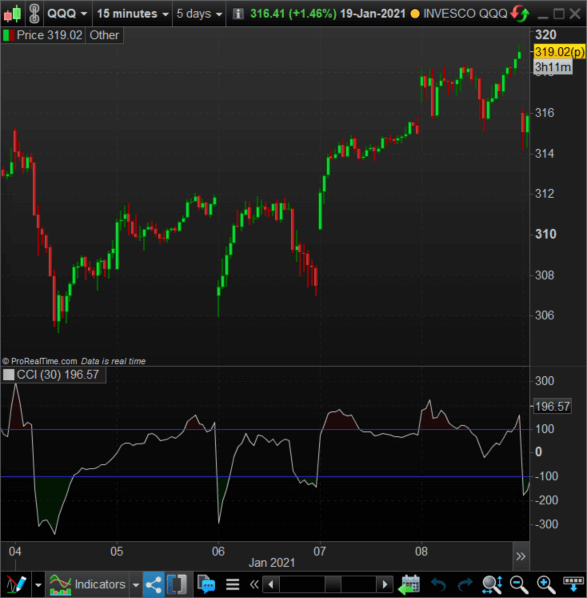
Aquí tenemos una gráfica de velas japonesas del ETF del Nasdaq. En la jerga de opciones, el precio que vemos en pantalla es el precio del subyacente.
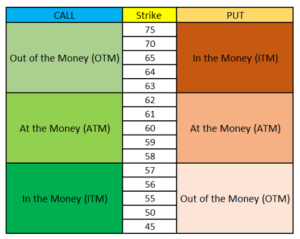
2. El precio de strike del contrato de opciones
El segundo parámetro es el precio de strike del call o del put con el que vayamos a operar.
Así pues, en primer lugar, tenemos que elegir qué contrato vamos a tomar antes de implementarlo sobre la formula Black Scholes. Si, por ejemplo, siguiendo el ejemplo de Microsoft, tomamos el contrato call a precio de strike de 220 $, ese será el valor que introduciremos en la calculadora.
Si quieres saber más sobre cómo funcionan las relaciones entre los precios de subyacente y de strike entre sí, puedes investigar más aquí.
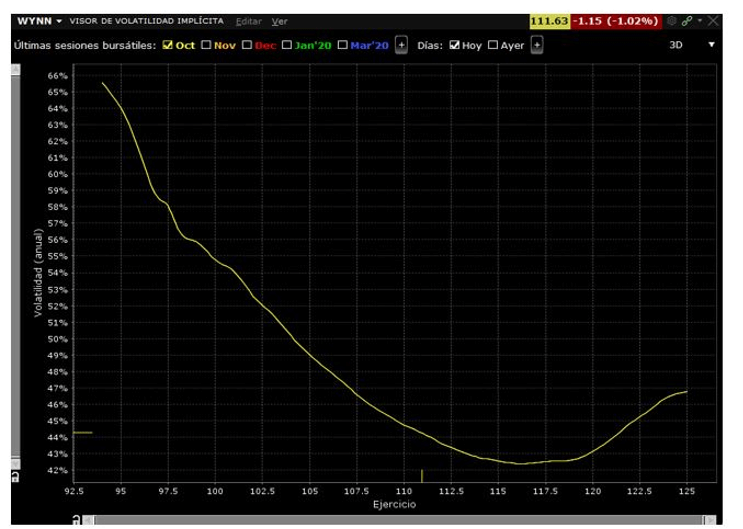
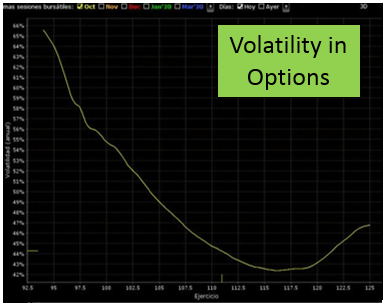
3. La volatilidad implícita
Este es otro de los parámetros más importantes que tenemos que tener en cuenta a la hora de realizar el trading de opciones, puesto que es el que más problemas va a producirnos a lo largo de nuestra carrera como traders de opciones.
La volatilidad implícita que debemos tomar a la hora de calcular el modelo de Black Scholes es la correspondiente al contrato de strike que hayamos tomado. Sin embargo, deberemos tomar la del lado comprador si pretendemos adquirir un contrato o la del lado vendedor si buscamos venderlo.
Este dato normalmente aparece en las cadenas de opciones cuando tratamos de realizar las operaciones, puesto que es de suma importancia a la hora de operar.
Si no sabes muy bien que es la volatilidad implícita o como tratarla, en este otro artículo puedes ver cómo funciona.
4. El factor temporal
El factor del tiempo es el cuarto factor que necesitaremos para determinar el cálculo de la prima de la opción en el modelo de Black Scholes.
Este dato podremos tomarlo directamente de la cadena de opciones, observando la fecha de vencimiento a la que expira el contrato de opciones con el que pretendemos operar.
Para poder introducirlo en la fórmula, primero hay que dividir el número de días hasta el vencimiento por el número de días del año en curso. Es decir, si tenemos un contrato que vence en 30 días, el dato que deberemos introducir será 30/365 días para poder replicar correctamente la fórmula de Black Scholes para opciones financieras.
5. Los tipos de interés
Los tipos de interés forman el quinto parámetro necesario para poder replicar el modelo de Black Scholes en opciones financieras.
Aunque este dato no es muy relevante a la hora de operar y no influye en gran medida en el modelo, sí que es necesario si queremos replicarlo correctamente.
Los tipos de interés podremos encontrarlos, o bien buscando en el navegador de internet o bien algunos brókeres los proveen directamente dentro de sus aplicaciones de trading de opciones.
Si te gustaría saber más sobre cómo afectan los tipos de interés a las opciones financieras, echa un vistazo a este artículo sobre la griega rho.
¿Acabas de iniciarte en opciones o todavía encuentras algunos conceptos confusos?  Con la serie de libros de Trading de Opciones para Todos aprenderás todo lo que necesitas saber para dominar el mercado de opciones |
6. El dividendo
El último parámetro que conforma el modelo de Black Scholes es el dividendo que reparte el fondo de inversiones o la empresa en cuestión sobre la que tratamos de operar con opciones. Por supuesto, si el subyacente con el que estamos tratando no repartiera dividendo alguno, su valor en la calculadora sería de cero.
Para encontrar el valor del dividendo que se reparte, podremos hacerlo buscando en cualquier periódico financiero o consultando la información que nos proporcione el bróker sobre el dividendo en cuestión.
Al igual que con los tipos de interés, el dividendo no juega un papel muy importante a la hora de establecer el valor de la prima de la opción. Sin embargo, al igual que antes es necesario para replicar estrictamente el modelo de Black Scholes.
¿Cuál es la fórmula del modelo de Black Scholes para opciones financieras?
Ahora que ya hemos descrito los seis parámetros, veremos las fórmulas necesarias para poder replicar el modelo Black and Scholes y calcular así el precio de la opción.
¿Cómo calcular d1 y d2 Black-Scholes?
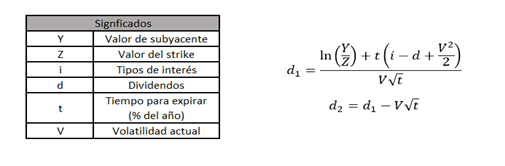
En primer lugar, vamos a necesitar dos parámetros auxiliares llamados d1 y d2. Estos se obtiene como sigue:
En este caso “ln” es el logaritmo Neperiano y “t” es el porcentaje de tiempo hasta el vencimiento, que se calculaba dividiendo el número de días al vencimiento entre el número de días del año.
Formula call Black Scholes y fórmula put Black Scholes
Ahora que ya hemos calculado d1 y d2 en Black Scholes, el siguiente paso consiste en obtener las fórmulas que gobiernan los precios del call y del put. Esto se hace a través de la siguiente expresión.
En este caso, “N(d1)” y “N(d2)” son la distribución Normal o Gaussiana con media igual a cero y desviación estándar igual a uno.
Esta es la manera de obtener una calculadora de opciones que replica el modelo de Black Scholes, aunque todavía hay más información que deberíamos añadir para que fuera completo. Para poder obtener un buen modelo Black and Scholes, deberemos añadir las griegas de las opciones a nuestra calculadora.
Si quieres saber cómo hacerlo, en esta sección podrás ver cómo obtener cada una de las fórmulas de las griegas de las opciones.
La calculadora de opciones financieras gratuita que replica el modelo de Black Scholes
Como has podido comprobar, replicar el modelo de Black Scholes es algo complejo, pero la buena noticia es que una vez está hecho, este modelo nos va a proporcionar la prima de cualquier opción, siendo extremadamente útil a la hora de operar.
black-scholes» width=»740″ height=»187″ />
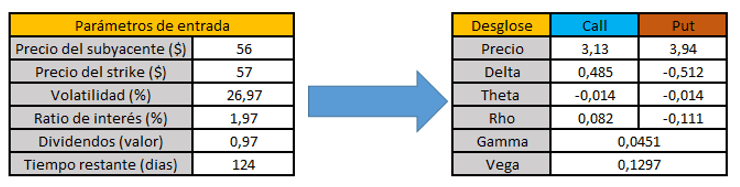
Para facilitarte las cosas, aquí puedes descargar el Excel que replica el modelo de Black Scholes que hemos empleado de ejemplo, junto con nuestra Guía de Opciones financieras, de manera completamente gratuita.
¿Por qué es importante tener una calculadora de opciones que replica el modelo Black Scholes?
Tener una réplica del modelo de Black Scholes es realmente importante porque hay veces en las que los mercados nos muestran unas primas en las cadenas de opciones que no se corresponden con la realidad.
Esto se debe a los bajos volúmenes de intercambio de contratos que suelen existir en las cadenas de opciones, y es posible que a veces tengamos que pagar mucho más de lo que en realidad deberíamos debido a que se genera un spread bid-ask demasiado amplio.
Para evitar este tipo de situaciones, es imprescindible tener una calculadora que replique el modelo de Black Scholes a mano, puesto que podremos ver la veracidad de las primas.
